In this activity, students construct their own rocket-powered boat called an "aqua-thruster." These aqua-thrusters will be made from a film canister and will use carbon dioxide gas produced from a chemical reaction between an antacid tablet and water to propel it. Students observe the effect that surface area of this simulated solid rocket fuel has on thrust.

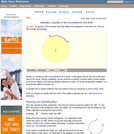
An interactive applet and associated web page that demonstrate the concept of an arc. The applet shows a circle with part of it highlighted to identify the arc. Each endpoint of the arc can be dragged to resize it. The web page has definitions and links to the properties of an arc. Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.

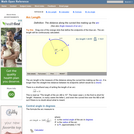
An interactive applet and associated web page that demonstrate the concept of arc length. The applet shows a circle with part of its circumference highlighted and the central angle shown. As the user drags either end of the arc it is redrawn and the calculation for arc length changes as you drag. The text on the web page gives the formula for calculating the arc length. Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.

The famous story of Archimedes running through the streets of Syracuse (in Sicily during the third century bc) shouting ''Eureka!!!'' (I have found it) reportedly occurred after he solved this problem. The problem combines the ideas of ratio and proportion within the context of density of matter.

Students create four-legged walking robots and measure how far they travel across different types of surfaces. They design and create "shoes" to add to the robots' feet and observe the effect of their modifications on the net distance traveled across the various surface types. This activity illustrates how the specialized locomotive features of different species help them to survive or thrive in their habitat environments. The activity is best as an enrichment tool that follows a lesson that introduces the concept of biological adaptation to students.

In this problem, students are given a picture of two triangles that appear to be similar, but whose similarity cannot be proven without further information. Asking students to provide a sequence of similarity transformations that maps one triangle to the other focuses them on the work of standard G-SRT.2, using the definition of similarity in terms of similarity transformations.

The year is 2032 and your class has successfully achieved a manned mission to Mars! After several explorations of the Red Planet, one question is still being debated: "Is there life on Mars?" The class is challenged with the task of establishing criteria to help look for signs of life. Student explorers conduct a scientific experiment in which they evaluate three "Martian" soil samples and determine if any contain life.

Create your own shapes using colorful blocks and explore the relationship between perimeter and area. Compare the area and perimeter of two shapes side-by-side. Challenge yourself in the game screen to build shapes or find the area of funky figures. Try to collect lots of stars!

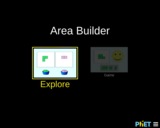
This simulation gives students the opportunity to explore both area and perimeter of 2-dimensional shapes. Students can explore by creating shapes and having the sim calculate the area and perimeter. They can also play a game where the goal is to create a shape with a specified area or area and perimeter, or to calculate the area and/or perimeter of a given shape.

Build rectangles of various sizes and relate multiplication to area. Discover new strategies for multiplying algebraic expressions. Use the game screen to test your multiplication and factoring skills!

This is a lesson for learning about area and perimeter of rectangles.

This corresponds to "College and Career Ready" standard (3.MD.7a) -- Find the area of a rectangle with whole-number side lengths by tiling it, and show that the area is the same as would be found by multiplying the side lengths.
(I was not able to find that standard here.)

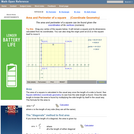
An interactive applet and associated web page showing how to find the area and perimeter of a square from the coordinates of its vertices. The square can be either parallel to the axes or rotated. The grid and coordinates can be turned on and off. The area and perimeter calculation can be turned off to permit class exercises and then turned back on the verify the answers. The applet can be printed as it appears on the screen to make handouts. The web page has a full description of the method for determining area and perimeter, a worked example and has links to other pages relating to coordinate geometry. Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.

An interactive applet and associated web page that demonstrate the area of a circle. A circle is shown with a point on the circumference that can be dragged to resize the circle. As the circle is resized, the radius and the area computation is shown changing in real time. The radius and formula can be hidden for class discussion. Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.

An interactive applet and associated web page that demonstrate the area of an ellipse. The major and minor axes can be dragged and the area is continuously recalculated. The ellipse has a grid inside it so that students can estimate the area and compare the result to the calculated one. The web page has the formula for the area calculation. The web page also has links to other pages defining the various properties of an ellipse and to some ellipse constructions. Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.

Overview: Math in Real Life (MiRL) supports the expansion of regional networks to create an environment of innovation in math teaching and learning.  The focus on applied mathematics supports the natural interconnectedness of math to other disciplines while infusing relevance for students.  MiRL supports a limited number of networked math learning communities that focus on developing and testing applied problems in mathematics.  The networks help math teachers refine innovative teaching strategies with the guidance of regional partners and the Oregon Department of Education.

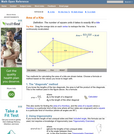
An interactive applet and associated web page that deals with the area of a kite, (a quadrilateral with two distinct pairs of equal adjacent sides). The applet shows a kite and the user can reshape it by dragging any vertex. The other vertices move automatically to ensure it always remains a kite. As the vertices are dragged, the area is continuously recalculated and displayed. The kite is filled with a grid of unit squares so that the students can estimate the area. The on-screen calculation can be hidden until the estimates are done. The web page lists two different ways to compute the area of a kite. Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.

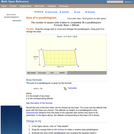
A web page and interactive applet showing the ways to calculate the area of a parallelogram. The user can drag the vertices of the parallelogram and the other points change automatically to ensure it remains a parallelogram. A grid inside the shape allows students to estimate the area visually, then check against the actual computed area, which is continuously recomputed and displayed. The text on the page gives three different ways to calculate the area with a formula for each. The applet uses one of the methods to compute the area in real time, so it changes as the rhombus is reshaped with the mouse. A companion page is http://www.mathopenref.com/parallelogram.html showing the definition and properties of a parallelogram Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.

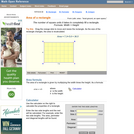
A web page and interactive applet showing the ways to calculate the area of a rectangle. The user can drag the vertices of the rectangle and the other points change automatically to ensure it remains a rectangle. A grid inside the shape allows students to estimate the area visually, then check against the actual computed area. The text on the page gives three different ways to calculate the area with a formula for each. The applet uses one of the methods to compute the area in real time, so it changes as the rectangle is reshaped with the mouse. A companion page is http://www.mathopenref.com/rectangle.html showing the definition and properties of a rectangle Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.

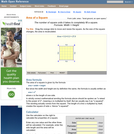
An interactive applet and associated web page that demonstrate the area of a square. The applet shows a square with all vertices draggable. As you drag any one, the area id continuously calculated and shown on the applet. The square is filled with a unit grid to allow class estimation of area. The displayed calculation can be turned off. Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.