Project Based Learning for Algebra 1 Students. Students must collect, analyze, and graph date.

"Students connect polynomial arithmetic to computations with whole numbers and integers.  Students learn that the arithmetic of rational expressions is governed by the same rules as the arithmetic of rational numbers.  This unit helps students see connections between solutions to polynomial equations, zeros of polynomials, and graphs of polynomial functions.  Polynomial equations are solved over the set of complex numbers, leading to a beginning understanding of the fundamental theorem of algebra.  Application and modeling problems connect multiple representations and include both real world and purely mathematical situations.

Find the rest of the EngageNY Mathematics resources at https://archive.org/details/engageny-mathematics.

"In this module, students synthesize and generalize what they have learned about a variety of function families.  They extend the domain of exponential functions to the entire real line (N-RN.A.1) and then extend their work with these functions to include solving exponential equations with logarithms (F-LE.A.4).  They explore (with appropriate tools) the effects of transformations on graphs of exponential and logarithmic functions.  They notice that the transformations on a graph of a logarithmic function relate to the logarithmic properties (F-BF.B.3).  Students identify appropriate types of functions to model a situation.  They adjust parameters to improve the model, and they compare models by analyzing appropriateness of fit and making judgments about the domain over which a model is a good fit.  The description of modeling as, “the process of choosing and using mathematics and statistics to analyze empirical situations, to understand them better, and to make decisions,” is at the heart of this module.  In particular, through repeated opportunities in working through the modeling cycle (see page 61 of the CCLS), students acquire the insight that the same mathematical or statistical structure can sometimes model seemingly different situations.

Find the rest of the EngageNY Mathematics resources at https://archive.org/details/engageny-mathematics."

(Nota: Esta es una traducción de un recurso educativo abierto creado por el Departamento de Educación del Estado de Nueva York (NYSED) como parte del proyecto "EngageNY" en 2013. Aunque el recurso real fue traducido por personas, la siguiente descripción se tradujo del inglés original usando Google Translate para ayudar a los usuarios potenciales a decidir si se adapta a sus necesidades y puede contener errores gramaticales o lingüísticos. La descripción original en inglés también se proporciona a continuación.)

"Los estudiantes conectan la aritmética polinomial con los cálculos con números enteros e enteros. Los estudiantes aprenden que la aritmética de las expresiones racionales se rige por las mismas reglas que la aritmética de los números racionales. Esta unidad ayuda a los estudiantes a ver conexiones entre soluciones a ecuaciones polinomiales, ceros de polinomiales,, y gráficos de funciones polinómicas. Las ecuaciones polinomiales se resuelven sobre el conjunto de números complejos, lo que lleva a una comprensión inicial del teorema fundamental del álgebra. Los problemas de aplicación y modelado conectan múltiples representaciones e incluyen situaciones de mundo real y puramente matemáticas.

Encuentre el resto de los recursos matemáticos de Engageny en https://archive.org/details/engageny-mathematics.

English Description:
"Students connect polynomial arithmetic to computations with whole numbers and integers.  Students learn that the arithmetic of rational expressions is governed by the same rules as the arithmetic of rational numbers.  This unit helps students see connections between solutions to polynomial equations, zeros of polynomials, and graphs of polynomial functions.  Polynomial equations are solved over the set of complex numbers, leading to a beginning understanding of the fundamental theorem of algebra.  Application and modeling problems connect multiple representations and include both real world and purely mathematical situations.

Find the rest of the EngageNY Mathematics resources at https://archive.org/details/engageny-mathematics.

(Nota: Esta es una traducción de un recurso educativo abierto creado por el Departamento de Educación del Estado de Nueva York (NYSED) como parte del proyecto "EngageNY" en 2013. Aunque el recurso real fue traducido por personas, la siguiente descripción se tradujo del inglés original usando Google Translate para ayudar a los usuarios potenciales a decidir si se adapta a sus necesidades y puede contener errores gramaticales o lingüísticos. La descripción original en inglés también se proporciona a continuación.)

"En este módulo, los estudiantes sintetizan y generalizan lo que han aprendido sobre una variedad de familias de funciones. Extienden el dominio de las funciones exponenciales a toda la línea real (n-rn.a.1) y luego extienden su trabajo con estas funciones a incluir la resolución de ecuaciones exponenciales con logaritmos (F-le.a.4). Exploran (con herramientas apropiadas) los efectos de las transformaciones en gráficos de funciones exponenciales y logarítmicas. Notan que las transformaciones en un gráfico de una función logarítmica se relacionan con el Propiedades logarítmicas (F-BF.B.3). Los estudiantes identifican tipos apropiados de funciones para modelar una situación. Ajustan los parámetros para mejorar el modelo y comparan los modelos analizando la idoneidad del ajuste y las juicios sobre el dominio sobre el cual un modelo es un buen ajuste. La descripción del modelado como, el proceso de elegir y usar matemáticas y estadísticas para analizar situaciones empíricas, comprenderlas mejor y tomar decisiones, está en el corazón de este módulo. En particular, a través de oportunidades repetidas para trabajar a través del ciclo de modelado (consulte la página 61 del CCLS), los estudiantes adquieren la idea de que la misma estructura matemática o estadística a veces puede modelar situaciones aparentemente diferentes.

Encuentre el resto de los recursos matemáticos de Engageny en https://archive.org/details/engageny-mathematics ".

English Description:
"In this module, students synthesize and generalize what they have learned about a variety of function families.  They extend the domain of exponential functions to the entire real line (N-RN.A.1) and then extend their work with these functions to include solving exponential equations with logarithms (F-LE.A.4).  They explore (with appropriate tools) the effects of transformations on graphs of exponential and logarithmic functions.  They notice that the transformations on a graph of a logarithmic function relate to the logarithmic properties (F-BF.B.3).  Students identify appropriate types of functions to model a situation.  They adjust parameters to improve the model, and they compare models by analyzing appropriateness of fit and making judgments about the domain over which a model is a good fit.  The description of modeling as, “the process of choosing and using mathematics and statistics to analyze empirical situations, to understand them better, and to make decisions,” is at the heart of this module.  In particular, through repeated opportunities in working through the modeling cycle (see page 61 of the CCLS), students acquire the insight that the same mathematical or statistical structure can sometimes model seemingly different situations.

Find the rest of the EngageNY Mathematics resources at https://archive.org/details/engageny-mathematics."

Students create and analyze composite materials with the intent of using the materials to construct a structure with optimal strength and minimal density. The composite materials are made of puffed rice cereal, marshmallows and chocolate chips. Student teams vary the concentrations of the three components to create their composite materials. They determine the material density and test its compressive strength by placing weights on it and measuring how much the material compresses. Students graph stress vs. strain and determine Young's modulus to analyze the strength of their materials.

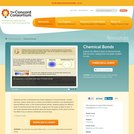
This interactive activity helps learners visualize the role of electrons in the formation of ionic and covalent chemical bonds. Students explore different types of chemical bonds by first viewing a single hydrogen atom in an electric field model. Next, students use sliders to change the electronegativity between two atoms -- a model to help them understand why some atoms are attracted. Finally, students experiment in making their own models: non-polar covalent, polar covalent, and ionic bonds. This item is part of the Concord Consortium, a nonprofit research and development organization dedicated to transforming education through technology.

This is a challenging task, suitable for extended work, and reaching into a deep understanding of units. The task requires students to exhibit MP1, Make sense of problems and persevere in solving them. An algebraic solution is possible but complicated; a numerical solution is both simpler and more sophisticated, requiring skilled use of units and quantitative reasoning. Thus the task aligns with either A-CED.1 or N-Q.1, depending on the approach.

Students' eyes are opened to the value of creative, expressive and succinct visual presentation of data, findings and concepts. Student pairs design, redesign and perform simple experiments to test the differences in thermal conductivity (heat flow) through different media (foil and thin steel). Then students create visual diagrams of their findings that can be understood by anyone with little background on the subject, applying their newly learned art vocabulary and concepts to clearly communicate their results. The principles of visual design include contrast, alignment, repetition and proximity; the elements of visual design include an awareness of the use of lines, color, texture, shape, size, value and space. If students already have data available from other experiments, have them jump right into the diagram creation and critique portions of the activity.

Modeling Our World with Mathematics Unit 2: Environmental Science Topic 2 - Sustainable Forestry

Modeling Our World with Mathematics Unit 4: Finances for Life Topic 2 - Loans and Consumer Credit

Students learn about the separation techniques of sedimentation and centrifugation and investigate whether blood is a homogeneous or a heterogeneous mixture. Working in groups as if they are biomedical researchers, they employ the scientific method and make observations about the known characteristics of urine, milk and blood. They probe further by analyzing research on the properties and fractionation modes of blood. As students learn about certain strange characteristics with the fractionation behavior of blood, they formulate hypotheses on the unique nature of blood. Using provided materials —olive oil, tomato juice and petroleum jelly—they design an experiment and construct a blood model. They test their hypotheses by conducting experiments on the blood model, and then propose theories for the nature of blood as a mixture—arriving at the theory of mixture dualism in blood—that blood is a complex mixture system. An activity-guiding handout and PowerPoint® presentation are provided for this student-directed, project-based activity.

This lesson unit is intended to help teachers assess how well students are able to: interpret a situation and represent the constraints and variables mathematically; select appropriate mathematical methods to use; make sensible estimates and assumptions; investigate an exponentially increasing sequence; and communicate their reasoning clearly.

This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: A small company wants to give raises to their 5 employees. They have $10,000 available to distribute. Imagine you are in charge of deciding how the rai...

The intent of clarifying statements is to provide additional guidance for educators to communicate the intent of the standard to support the future development of curricular resources and assessments aligned to the 2021 math standards.  Clarifying statements can be in the form of succinct sentences or paragraphs that attend to one of four types of clarifications: (1) Student Experiences; (2) Examples; (3) Boundaries; and (4) Connection to Math Practices.

Using paper, paper clips and tape, student teams design flying/falling devices to stay in the air as long as possible and land as close as possible to a given target. Student teams use the steps of the engineering design process to guide them through the initial conception, evaluation, testing and re-design stages. The activity culminates with a classroom competition and scoring to evaluate how each team's design performed.

Students are introduced to statics and dynamics, free-body diagrams, combustion and thermodynamics to gain an understanding of the forces needed to lift rockets off the ground. They learn that thrust force is needed to launch rockets into space and the energy for thrust is stored as chemical energy in the rocket's fuel. Then, using the law of conservation of energy, students learn that the chemical energy of the fuel is converted into work and heat energy during a rocket launch. A short PowerPoint® presentation is provided, including two example problems for stoichiometry review. An optional teacher demonstration is described as an extension activity.

The “Systems Are Everywhere” module was originally written for high school science teachers or counselors to use in any setting (in class or in extracurricular programs). However, during field-testing, we found that many elementary and middle school teachers were able to use these lessons successfully with their students. The module is made up of three lessons that serve to foster students’ understanding of systems, systems models, and systems thinking at every level of learning and across many content areas. Blended throughout the lessons are career connections that will introduce students to diverse systems thinkers in STEM, and provide context for how systems approaches are used in real life to address complex problems. The lessons and module can be used as a stand-alone set of activities or can be integrated into any course as an extension or enrichment.

The module begins with students modeling a complex system. Students will brainstorm and sketch the parts and connections of the system, then use an online tool (Loopy) to model the interactions of those parts and connections. Next, students will develop their understanding of systems thinking skills and their application for addressing problems and solutions. Then, students will apply their knowledge and skills to model a system of their choosing. Lastly, they will showcase their skills by creating a student profile and integrating their systems thinking skills into a resume.

Target Audience
This is our introductory module that we recommend teaching before each of our other modules to give students a background in systems and to help them understand the many careers available in STEM. This module can be applied easily to any content area and works best as written for students between 6th and 12th grades but can be adapted for other ages. It works very well when teaching virtually and in-person. If you are looking for an introduction to systems that can be delivered in-person with more kinesthetic activities, please see our Introduction to Systems module. The Intro to Systems module works best with 8-12 grade students, though can be used with some modifications for 6-7th graders. This Systems are Everywhere module can work well for elementary through secondary grades.

This task, while involving relatively simple arithmetic, codes to all three standards in this cluster, and also offers students a good opportunity to practice modeling (MP4), since they must attempt to make reasonable assumptions about the average length of vehicles in the traffic jam and the space between vehicles. Teachers can encourage students to compare their solutions with other students.