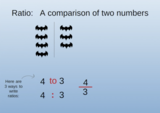
This lesson teaches about Rates, Ratios, and Unit Rates, using visually appealing art and real-life examples that will engage teenagers.
- Subject:
- Ratios and Proportions
- Material Type:
- Lesson
- Author:
- Janel Williams
- Date Added:
- 01/15/2021

This lesson teaches about Rates, Ratios, and Unit Rates, using visually appealing art and real-life examples that will engage teenagers.

In order to solve this problem, students must assume that if you mix a cubic foot of sand with a cubic foot of cement, you will have 2 cubic feet of mix.
![OREGON MATH STANDARDS (2021): [6.RP]](https://img.oercommons.org/160x134/oercommons/media/courseware/lesson/image/13138_ODE_Math_Logo_2018-H_color_BvjqVNy.png)
The intent of clarifying statements is to provide additional guidance for educators to communicate the intent of the standard to support the future development of curricular resources and assessments aligned to the 2021 math standards. Clarifying statements can be in the form of succinct sentences or paragraphs that attend to one of four types of clarifications: (1) Student Experiences; (2) Examples; (3) Boundaries; and (4) Connection to Math Practices.

This lesson unit is intended to help sixth grade teachers assess how well students are able to: Analyze a realistic situation mathematically; construct sight lines to decide which areas of a room are visible or hidden from a camera; find and compare areas of triangles and quadrilaterals; and calculate and compare percentages and/or fractions of areas.

The purpose of this task is to provide students an opportunity to use mathematics addressed in different standards in the same problem.
A task involving Ratios and Rates

The battle is on in this game where you build your own potions! Check your ratios to win this mixture mix-off. Ratio Rumble guides students in: identifying ratios when used in a variety of contextual situations; providing visual representations of ratios; solving common problems or communicating by using rate, particularly unit rates; and explaining why ratios and rates naturally relate to fractions and decimals.
In some textbooks, a distinction is made between a ratio, which is assumed to have a common unit for both quantities, and a rate, which is defined to be a quotient of two quantities with different units (e.g. a ratio of the number of miles to the number of hours). No such distinction is made in the common core and hence, the two quantities in a ratio may or may not have a common unit. However, when there is a common unit, as in this problem, it is possible to add the two quantities and then find the ratio of each quantity with respect to the whole (often described as a part-whole relationship).

In this task students use ratio and rate reasoning to solve the real-world problem of a runners rate and distance.

A very short video introduction to how photosynthesis cycles energy through an ecosystem and a "real-world" application of ratios! Lindsay Hollister, JPPM's horticulturalist, taps a black walnut tree for its sap and park staff boil it down to create syrup. Included in this video are an animated food web showing the directions of energy flow during photosynthesis and when sap is "rising," which can be extended by students to include humans or more parts of their local ecosystem. Use the video as an introduction to activities about sugar and biological storage, and an excuse to sample maple syrup to taste the sugar. Alternatively, research trees nearby students could help tap and witness the biological transfer of energy themselves.
Always be sure you can successfully identify a plant before using it and take precautions to avoid negative reactions.
This resource is part of Jefferson Patterson Park and Museum’s open educational resources project to provide history, ecology, archaeology, and conservation resources related to our 560 acre public park. More of our content can be found here on OER Commons or from our website at jefpat.maryland.gov. JPPM is a part of the Maryland Historical Trust under the Maryland Department of Planning.

Students will analyze ratios and use proportions to solve problems using a cooperative, kinesthetic activity in which they will create “human ratios.” Students will use ratios to compare two quantities, then solve problems cooperatively by demonstrating how proportions are written to show equivalent ratios.

In this task students use ratio and rate reasoning to solve the real-world problem of placing a security camara in a shop.

This lesson unit is intended to help teachers assess how well students are able to solve a real-world modeling problem. There are several correct approaches to the problem, including some that involve proportional relationships.
There is a 40% chance that the lower ⅓ of the of the Cascadia subduction zone will rupture in the next 50 years, generating a large earthquake and ensuing tsunami. In this project, students will work collaboratively to design and test a model of a vertical evacuation structure. They will evaluate the performance of their models and propose further modifications to improve their design. Students will then make a scale drawing and a model to apply math concepts of scale to designing and creating an ideal model of a vertical evacuation structure. Finally, students will present their findings and proposed final design to their peers and an adult audience. The entire process takes about 2 weeks, and was expanded to include more information and activities with earthquake/tsunami prediction and application of scale. The unit is a great fit for standards within Earth Science (specifically plate tectonics and human mitigation) as well as Engineering and Design standards.
Students should have prior knowledge of rates and solving proportions. Students will be introduced to a problem that launches the lesson. By the end of the lesson, students should be able to answer the launch question. During the lesson, students will explore finding the unit rate, watch a video demonstration, and practice via whiteboards and interactively.

Engineers design and implement many creative techniques for managing stormwater at its sources in order to improve and restore the hydrology and water quality of developed sites to pre-development conditions. Through the two lessons in this unit, students are introduced to green infrastructure (GI) and low-impact development (LID) technologies, including green roofs and vegetative walls, bioretention or rain gardens, bioswales, planter boxes, permeable pavement, urban tree canopies, rainwater harvesting, downspout disconnection, green streets and alleys, and green parking. Student teams take on the role of stormwater engineers through five associated activities. They first model the water cycle, and then measure transpiration rates and compare native plant species. They investigate the differences in infiltration rates and storage capacities between several types of planting media before designing their own media mixes to meet design criteria. Then they design and test their own pervious pavement mix combinations. In the culminating activity, teams bring together all the concepts as well as many of the materials from the previous activities in order to create and install personal rain gardens. The unit prepares the students and teachers to take on the design and installation of bigger rain garden projects to manage stormwater at their school campuses, homes and communities.

This problem is the fifth in a series of seven about ratios. In the first problem students define the simple ratios that exist among the three candidates. It opens an opportunity to introduce unit rates. The subsequent problems are more complex. In the second problem, students apply their understanding of ratios to combine two pools of voters to determine a new ratio. In the third problem, students apply a known ratio to a new, larger pool of voters to determine the number of votes that would be garnered.

This is the sixth problem in a series of seven that use the context of a classroom election. While it still deals with simple ratios and easily managed numbers, the mathematics surrounding the ratios are increasingly complex.

This is the last problem of seven in a series about ratios set in the context of a classroom election. Since the number of voters is not known, the problem is quite abstract and requires a deep understanding of ratios and their relationship to fractions.
This is the first and most basic problem in a series of seven problems, all set in the context of a classroom election. Every problem requires students to understand what ratios are and apply them in a context. The problems build in complexity and can be used to highlight the multiple ways that one can reason about a context involving ratios.