Grades 9-12 Personalized Learning Plan Algebra I, Algebra II, and Geometry Scope & Sequence

Explore the world of lines. Investigate the relationships between linear equations, slope, and graphs of lines. Challenge yourself in the line game!

Students are introduced to graphing on the coordinate plane, in the first quadrant, using (x, y) coordinates.

How are math, art, music, and language intertwined? How does intelligent behavior arise from its component parts? Can computers think? Can brains compute? Douglas Hofstadter probes very cleverly at these questions and more in his Pulitzer Prize winning book, “Gödel, Escher, Bach”. In this seminar, we will read and discuss the book in depth, taking the time to solve its puzzles, appreciate the Bach pieces that inspired its dialogues, and discover its hidden tricks along the way.

A web page and interactive applet illustrating the properties of a hexagon (6 sided polygon). The applet shows a hexagon where the user can drag any vertex to reshape it. User can see that the interior and exterior angles are constant in a regular hexagon, but vary in an irregular version. Controls allow the display or hiding of the diagonals, and triangles within the hexagon. The web page lists the properties of a hexagon including interior angles, exterior angles, sum of exterior angles, area, number of diagonals and number of internal triangles. Links to pages with generalized properties of all polygons. Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.

The goal of this task is to use geometry study the structure of beehives. Beehives have a tremendous simplicity as they are constructed entirely of small, equally sized walls. In order to as useful as possible for the hive, the goal should be to create the largest possible volume using the least amount of materials. In other words, the ratio of the volume of each cell to its surface area needs to be maximized. This then reduces to maximizing the ratio of the surface area of the cell shape to its perimeter.

This ½ credit Geometry class is designed as one component of Oregon’s “core 2” mathematics sequence for grade 9 and 10 students. In addition to this course, students should have access to 1 credit worth of Algebra standards and ½ credit of Data Reasoning.

This course is designed to be implemented by an instructor steeped in the four cornerstones of the Oregon Math Project. In particular, the course centers “belonging” in its design for heterogeneous, detracked classrooms and “engagement” as it anchors relevant and hands-on activities. Unit options are provided so that teachers can make informed decisions based on their unique contexts.

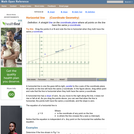
An interactive applet and associated web page that show the definition of a horizontal line in coordinate geometry. The applet has two points that the user can drag which define a line. The line flagged when it is horizontal (slope=0) and the equation of the line is shown. The grid, details and coordinates can be turned on and off. The applet can be printed exactly as it appears on the screen to make handouts. The web page has a discussion on how to test for horizontal, the line equation and has links to other pages relating to coordinate geometry. Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.

Students will customize a hot air balloon using a non-typical shape and calculate volume

The purpose of this task is for students to apply the concepts of mass, volume, and density in a real-world context. There are several ways one might approach the problem, e.g., by estimating the volume of a person and dividing by the volume of a cell.

This is a mathematical modeling task aimed at making a reasonable estimate for something which is too large to count accurately, the number of leaves on a tree.

In this problem, the variables a,b,c, and d are introduced to represent important quantities for this esimate: students should all understand where the formula in the solution for the number of leaves comes from. Estimating the values of these variables is much trickier and the teacher should expect and allow a wide range of variation here.

As written, this problem gives students all of the information they need to estimate the thickness of a soda can.

his is a version of ''How thick is a soda can I'' which allows students to work independently and think about how they can determine how thick a soda can is. The teacher should explain clearly that the goal of this task is to come up with an ''indirect'' means of assessing how thick the can is, that is directly measuring its thickness is not allowed.

Throughout this problem-based learning module students will address real world skills. Students will be asked to brainstorm ideas and think innovatively both independently and collaboratively in addressing a real-world problem that is relevant to their daily lives and surroundings.  Students/teams will be encouraged to use the internet for research purposes in their design phase. What components should be included for a modern, updated classroom? Students will utilize various online platforms to design an ideal, modern, contemporary “dream classroom”.  Students will incorporate components that would meet the needs of all learners and a classroom that would be able to integrate technology. These classrooms can be shared with relevant individuals in the community and others in the school building.

Throughout this problem-based learning module students will address real world skills. Students will be asked to brainstorm ideas and think innovatively both independently and collaboratively in addressing a real-world problem that is relevant to their daily lives and surroundings.  Students/teams will be encouraged to use the internet for research purposes in their design phase. What components should be included for a modern, updated classroom? Students will utilize various online platforms to design an ideal, modern, 21st century “dream classroom”.  Students will incorporate components that would meet the needs of all learners and a classroom that would be able to integrate technology. These classrooms can be shared with relevant individuals in the community and others in the school building.

An interactive applet and associated web page that provide step-by-step animated instructions on how to measure angles using a protractor. Specifically, it uses a protractor to measure two angles that form a vertical pair, verifying they have the same measure. The animation can be run either continuously like a video, or single stepped to allow classroom discussion and thought between steps. Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.

In dit college wordt een introductie gegeven van een groot aantal facetten van de scheepshydromechanica en hun onderlinge samenhang zoals die later in de studie meer als geisoleerde onderwerpen aan bod komen. Behandeld worden: de hydrostatica, de geometrie beschrijving van het schip, inleiding lijnenplan, het begrip stabiliteit, de stabiliteit van drijvende lichamen, eenvoudige stabiliteit berekening bij kleine helling hoeken, de weerstand van lichamen onder water en aan het oppervlak, eenvoudige weerstand benaderings methoden voor schepen, de model wetten in de hydromechanica, de extrapolatie methode van Froude, de lift van een vleugel, de vleugel karakteristieken, de toepassing hiervan bij voortstuwing en bij scheepsschroeven, de schroef karakteristieken en een eenvoudige schroef berekening, en tenslotte de fysica van het zeilen en zeilvoortstuwing. Leerdoelen De student kan: 1. de basis van systeem analyse beschrijven (buitenwereld, interfaces, beperkingen, objecten, relaties enz.) 2. maritieme systemen zoals schip/motor/schroef beschrijven en modelleren met behulp van beperkte systeem analyse methodologie; eenvoudige maritieme systemen modelleren door onderverdeling in subsystemen en componenten 3. evenwicht condities van maritieme systemen bepalen en kwalitatief analyseren 4. de definities en belangrijkste karakteristieken van weerstand, voortstuwing en manoeuvreren (snelheid, weerstand, vermogen, RPM, draaicapaciteit) begrijpen en toepassen 5. de relaties tussen algemeen vloeistof dynamica en scheepshydromechanica (bijv. lift/aerodynamica/zeilen; visceuze stroming/Reynolds getal/volgstroomvelden/voortstuwingsrendement; laminair & visceuze stroming/weerstand; niet visceuze stroming/golf patronen/weerstand) beschrijven 6. de achtergrond van de belangrijkste schaal regels (Newton, Froude, Reynolds) d.m.v dimensie analyse uitleggen 7. schaalregels voor schaalmodel experimenten in een sleeptank toepassen en potentiĚÇle complicaties identificeren

This rich task is an excellent example of geometric concepts in a modeling situation and is accessible to all students. In this task, students will provide a sketch of a paper ice cream cone wrapper, use the sketch to develop a formula for the surface area of the wrapper, and estimate the maximum number of wrappers that could be cut from a rectangular piece of paper.

This short video and interactive assessment activity is designed to teach third graders an overview of rectangles, squares, circles and triangles.