The purpose of this task is for students to apply the concepts of mass, volume, and density in a real-world context. There are several ways one might approach the problem, e.g., by estimating the volume of a person and dividing by the volume of a cell.
Material Type: Activity/Lab
This task combines two skills from domain G-C: making use of the relationship between a tangent segment to a circle and the radius touching that tangent segment (G-C.2), and computing lengths of circular arcs given the radii and central angles (G-C.5). It also requires students to create additional structure within the given problem, producing and solving a right triangle to compute the required central angles (G-SRT.8).
Material Type: Activity/Lab
The result here complements the fact, presented in the task ``Right triangles inscribed in circles I,'' that any triangle inscribed in a circle with one side being a diameter of the circle is a right triangle. A second common proof of this result rotates the triangle by 180 degrees about M and then shows that the quadrilateral, obtained by taking the union of these two triangles, is a rectangle.
Material Type: Activity/Lab
his is a version of ''How thick is a soda can I'' which allows students to work independently and think about how they can determine how thick a soda can is. The teacher should explain clearly that the goal of this task is to come up with an ''indirect'' means of assessing how thick the can is, that is directly measuring its thickness is not allowed.
Material Type: Activity/Lab
This task examines some of the properties of reflections of the plane which preserve an equilateral triangle: these were introduced in ''Reflections and Isosceles Triangles'' and ''Reflection and Equilateral Triangles I''. The task gives students a chance to see the impact of these reflections on an explicit object and to see that the reflections do not always commute.
Material Type: Activity/Lab
For these particular triangles, three reflections were necessary to express how to move from ABC to DEF. Sometimes, however, one reflection or two reflections will suffice. Since any rigid motion will take triangle ABC to a congruent triangle DEF, this shows the remarkable fact that any rigid motion of the plane can be expressed as one reflection, a composition of two reflections, or a composition of three reflections.
Material Type: Activity/Lab
This task can be implemented in a variety of ways. For a class with previous exposure to properties of perpendicular bisectors, part (a) could be a quick exercise in geometric constructions, and an application of the result. Alternatively, this could be part of an introduction to perpendicular bisectors, culminating in a full proof that the three perpendicular bisectors are concurrent at the circumcenter of the triangle, an essentially complete proof of which is found in the solution below.
Material Type: Activity/Lab
This task provides a good opportunity to use isosceles triangles and their properties to show an interesting and important result about triangles inscribed in a circle: the fact that these triangles are always right triangles is often referred to as Thales' theorem. It does not have a lot of formal prerequisites, just the knowledge that the sum of the three angles in a triangle is 180 degrees.
Material Type: Activity/Lab
This task is inspired by the derivation of the volume formula for the sphere. If a sphere of radius 1 is enclosed in a cylinder of radius 1 and height 2, then the volume not occupied by the sphere is equal to the volume of a Ňdouble-naped coneÓ with vertex at the center of the sphere and bases equal to the bases of the cylinder.
Material Type: Activity/Lab
This task applies geometric concepts, namely properties of tangents to circles and of right triangles, in a modeling situation. The key geometric point in this task is to recognize that the line of sight from the mountain top towards the horizon is tangent to the earth. We can then use a right triangle where one leg is tangent to a circle and the other leg is the radius of the circle to investigate this situation.
Material Type: Activity/Lab
The construction of the tangent line to a circle from a point outside of the circle requires knowledge of a couple of facts about circles and triangles. First, students must know, for part (a), that a triangle inscribed in a circle with one side a diameter is a right triangle. This material is presented in the tasks ''Right triangles inscribed in circles I.'' For part (b) students must know that the tangent line to a circle at a point is characterized by meeting the radius of the circle at that point in a right angle: more about this can be found in ''Tangent lines and the radius of a circle.''
Material Type: Activity/Lab
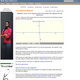
This task provides a construction of the angle bisector of an angle by reducing it to the bisection of an angle to finding the midpoint of a line segment. It is worth observing the symmetry -- for both finding midpoints and bisecting angles, the goal is to cut an object into two equal parts. The conclusion of this task is that they are, in a sense, of exactly equivalent difficulty -- bisecting a segment allows us to bisect and angle (part a) and, conversely, bisecting an angle allows us to bisect a segment (part b). In addition to seeing how these two constructions are related, the task also provides an opportunity for students to use two different triangle congruence criteria: SSS and SAS.
Material Type: Activity/Lab
An interactive applet and associated web page that illustrate the triangles that can be drawn inside a polygon. The applet has a pentagon with the triangles drawn. The user can change the number of sides, and switch between regular / irregular. The vertices are draggable. The text on the page discusses the uses of these triangles. Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.
Material Type: Reading, Simulation
An interactive applet and associated web page that demonstrate a bisector of a line segment. The applet shows a fixed line segment and another line that bisects it. The second line's endpoints can be dragged, but the line adjusts itself so that it always bisects the fixed line. Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.
Material Type: Reading, Simulation
An interactive applet and associated web page that provide step-by-step instructions on how to bisect an angle using only a compass and straightedge. The animation can be run either continuously like a video, or single stepped to allow classroom discussion and thought between steps. Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.
Material Type: Reading, Simulation
An interactive applet and associated web page that provide step-by-step instructions on how to copy a line segment using only a compass and straightedge. The animation can be run either continuously like a video, or single stepped to allow classroom discussion and thought between steps. Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.
Material Type: Reading, Simulation
An interactive applet and associated web page that demonstrate the bisector of an angle. An angle is shown using two line segments that can be dragged to change the angle measure. The angle is bisected by a line which moves while dragging to always divide the angle into two equal angles. The angle measures can be turned off for class discussions. Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.
Material Type: Reading, Simulation
An interactive applet and associated web page that demonstrate the concept of an arc. The applet shows a circle with part of it highlighted to identify the arc. Each endpoint of the arc can be dragged to resize it. The web page has definitions and links to the properties of an arc. Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.
Material Type: Reading, Simulation
An interactive applet and associated web page that demonstrate the definition of a line. The applet presents two points and a line that passes through them extending to infinity in both directions. As the points a re dragged the line moves but it is never possible to reveal a line end. See also the entries for line segment and ray. Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.
Material Type: Reading, Simulation
An interactive applet and associated web page that provide step-by-step animated instructions on how to construct a line parallel to a given line through a given point off the line. The animation can be run either continuously like a video, or single stepped to allow classroom discussion and thought between steps. Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.
Material Type: Reading, Simulation
