All resources in Oregon Mathematics

Search

When Does SSA Work to Determine Triangle Congruence?

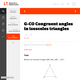
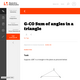
(View Complete Item Description)

The triangle congruence criteria, SSS, SAS, ASA, all require three pieces of information. It is interesting, however, that not all three pieces of information about sides and angles are sufficient to determine a triangle up to congruence. In this problem, we considered SSA. Also insufficient is AAA, which determines a triangle up to similarity. Unlike SSA, AAS is sufficient because two pairs of congruent angles force the third pair of angles to also be congruent.

Material Type: Activity/Lab

Author: Illustrative Mathematics

G-CO Classifying Triangles

(View Complete Item Description)

This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Choose two distinct points $A$ and $B$ in the plane. For which points $C$ is $\triangle ABC$ a right triangle? For which points $C$ is $\triangle ABC$ ...

Material Type: Activity/Lab

Author: Illustrative Mathematics

Locating Warehouse

(View Complete Item Description)

This task can be implemented in a variety of ways. For a class with previous exposure to the incenter or angle bisectors, part (a) could be a quick exercise in geometric constructions,. Alternatively, this could be part of a full introduction to angle bisectors, culminating in a full proof that the three angle bisectors are concurrent, an essentially complete proof of which is found in the solution below.

Material Type: Activity/Lab

Author: Illustrative Mathematics

G-CO Origami equilateral triangle

(View Complete Item Description)

This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Jessica is working to construct an equilateral triangle with origami paper and uses the following steps. First she folds the paper in half and then unf...

Material Type: Activity/Lab

Author: Illustrative Mathematics

G-CO Origami regular octagon

(View Complete Item Description)

This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Lisa makes an octagon by successively folding a square piece of paper as follows. First, she folds the square in half vertically and horizontally and a...

Material Type: Activity/Lab

Author: Illustrative Mathematics

G-GMD Area of a circle

(View Complete Item Description)

This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: The goal of this task is to explain why the area enclosed by a circle $C$ of radius $r$ is $\pi r^2$. Recall that $\pi$ is the ratio of the circumferen...

Material Type: Activity/Lab

Author: Illustrative Mathematics

G-GMD Circumference of a circle

(View Complete Item Description)

This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Suppose we define $\pi$ to be the circumference of a circle whose diameter is 1: Explain why the circumference of a circle with radius $r \gt 0$ is $2\...

Material Type: Activity/Lab

Author: Illustrative Mathematics

Centerpiece

(View Complete Item Description)

The purpose of this task is to use geometric and algebraic reasoning to model a real-life scenario. In particular, students are in several places (implicitly or explicitly) to reason as to when making approximations is reasonable and when to round, when to use equalities vs. inequalities, and the choice of units to work with (e.g., mm vs. cm).

Material Type: Activity/Lab

Author: Illustrative Mathematics

Doctor's Appointment

(View Complete Item Description)

The purpose of the task is to analyze a plausible real-life scenario using a geometric model. The task requires knowledge of volume formulas for cylinders and cones, some geometric reasoning involving similar triangles, and pays attention to reasonable approximations and maintaining reasonable levels of accuracy throughout.

Material Type: Activity/Lab

Author: Illustrative Mathematics

G-GMD Volume Estimation

(View Complete Item Description)

This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Charles and Olivia are trying to estimate the volume of water that could be held by the figure shown below, which is 10 feet high and has a circular to...

Material Type: Activity/Lab

Author: Illustrative Mathematics

G-SRT, G-MG How far is the horizon?

(View Complete Item Description)

This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Milong and her friends are at the beach looking out onto the ocean on a clear day and they wonder how far away the horizon is. About how far can Milong...

Material Type: Activity/Lab

Author: Illustrative Mathematics

Paper Clip

(View Complete Item Description)

This high level task is an example of applying geometric methods to solve design problems and satisfy physical constraints. This task is accessible to all students. In this task, a typographic grid system serves as the background for a standard paper clip.

Material Type: Activity/Lab

Author: Illustrative Mathematics

Load more