
This modeling task is focused on finding rectilinear area of two figures.
- Subject:
- Education
- Elementary Education
- Mathematics
- Measurement and Data
- Material Type:
- Activity/Lab
- Assessment
- Homework/Assignment
- Date Added:
- 08/16/2018


This modeling task is focused on finding rectilinear area of two figures.
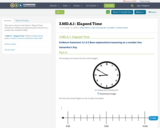
This task is related to Sub Claim C: Elapsed Time. Students are adding and subtracting time intervals on a number line. Standard 3.MD.1
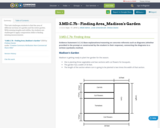
This task challenges students to find the area of different sections of a garden and the entire garden. With missing lengths and widths, the students are challenged to apply computation skills to finding missing measurements.
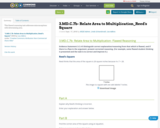
This flawed reasoning task addresses misconceptions with determining area.

This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Find the area of each colored figure. Each grid square is 1 inch long....
This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important aspects of the task and its potential use.

This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important aspects of the task and its potential use.

This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important aspects of the task and its potential use.
Write and/or solve linear equations in one variable.
b. Write and/or solve two-step equations of the form px + q = r and p(x + q) = r, where p, q and r are rational numbers, and interpret the meaning of the solution in the context of the problem.

This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Plot the following numbers on the number line: 80 328 791 1. Round each number to the nearest 100. How can you see this on the number line? 2. Round ea...

This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: There are 6 tables in Mrs. Potter's art classroom. There are 4 students sitting at each table. Each student has a box of 10 colored pencils. (A) How ma...

This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Plot 8, 32, and 79 on the number line. 1. Round each number to the nearest 10. How can you see this on the number line? 2. Round each number to the nea...
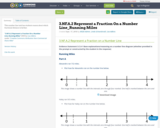
This number line task has students reason about which fractional distance is farther.
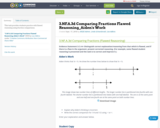
This task provides students practice with flawed reasoning using fraction comparisons.

This flawed reasoning task provides practice for students to understand the size of the wholes must be equal in order to compare fractions.

This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Choose each statement that is true. $\frac34$ is greater than $\frac54$. $\frac54$ is greater than $\frac34$. $\frac34 \gt \frac54$. $\frac34 \lt \frac...

This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: Choose each statement that is true. $\frac98$ is greater than $\frac{9}{4}$. $\frac{9}{4}$ is greater than $\frac98$. $\frac98 \gt \frac{9}{4}$. $\frac...

This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: The number line below shows two numbers, 0 and 1. Where is $\frac14$ on this number line? http://www.youtube.com/watch?v=HJ0LDgxVGfU...

This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: The number line below shows two numbers, 0 and $\frac53$. Where is 1 on this number line? http://www.youtube.com/watch?v=wAXRjMUgiu4...

This is a task from the Illustrative Mathematics website that is one part of a complete illustration of the standard to which it is aligned. Each task has at least one solution and some commentary that addresses important asects of the task and its potential use. Here are the first few lines of the commentary for this task: The number line below shows two numbers, 0 and 1. Where is $\frac74$ on this number line? http://www.youtube.com/watch?v=TEzH_PbHZIw...