This lesson unit is intended to help teachers assess how well students are able to: solve linear equations in one variable with rational number coefficients; collect like terms; expand expressions using the distributive property; and categorize linear equations in one variable as having one, none, or infinitely many solutions. It also aims to encourage discussion on some common misconceptions about algebra.

This lesson unit is intended to help teachers assess how well students are able to formulate and solve problems using algebra and, in particular, to identify and help students who have the following difficulties: solving a problem using two linear equations with two variables; and interpreting the meaning of algebraic expressions.

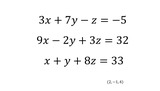
Linear equations in three variables are, in theory, solvable by hand. Using Gaussian elimination.
That is great, except that sometimes just CANNOT seem to get the answer.
In that case, a TI-84 can do this for you.

The purpose of this task is to show how the ideas in the RP and EE domains in 6th and 7th grade mature in 8th grade.

This lesson unit is intended to help teachers assess how well students are able to: form and solve linear equations involving factorizing and using the distributive law. In particular, this unit aims to help teachers identify and assist students who have difficulties in: using variables to represent quantities in a real-world or mathematical problem and solving word problems leading to equations of the form px + q = r and p(x + q) = r.

This seminar will explore how to solve a system of linear equations using substitution. It will also describe what it means for a system of equations to have no solution or infinitely many solutions.  Applications of systems of equations will also be explored.StandardsCC.2.2.HS.D.10Represent, solve, and interpret equations/inequalities and systems of equations/inequalities algebraically and graphically.

In this task, we are given the graph of two lines including the coordinates of the intersection point and the coordinates of the two vertical intercepts, and are asked for the corresponding equations of the lines. It is a very straightforward task that connects graphs and equations and solutions and intersection points.

     This problem-based learning module is designed to link a student’s real-life problem to learning targets in the subjects of math, social studies and language arts.  The problem being, what route is best for me to buy a vehicle?  The students will prepare, research and present findings about their own personal finances relating to buying a vehicle.  The students will create two equations based on two purchasing plans they will be comparing.  At the conclusion, students will be able to decide which plan is best for them based on research and mathematical practices.  Students will present to their peers, teachers, administrators, and most importantly their parents in an attempt to convince them of their chosen plan.    This blended module includes teacher led instruction, student led rotations, community stakeholder collaboration and technology integration.