This 23-minute video provides an introduction to viruses. [Biology playlist: Lesson 19 of 71].

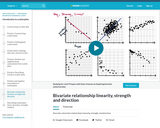
Describe a bivariate relationship's linearity, strength, and direction. In other words, plotting things that take two variables into consideration and trying to see whether there's a pattern with how they relate.

This is a brief conditional probability examplediscussing probabilities like P(A | B) using breakfast and lunch as examples.

The Calculus BC AP exam is a super set of the AB exam. It covers everything in AB as well as some of the more advanced topics in integration, sequences and function approximation. This tutorial is great practice for anyone looking to test their calculus mettle!

A single definite integral can be used to find the area under a curve. with double integrals, we can start thinking about the volume under a surface!

This is about as many integrals we can use before our brains explode. Now we can sum variable quantities in three-dimensions (what is the mass of a 3-D wacky object that has variable mass)!

This 9-minute video lesson provides an introduction to L'Hopital's Rule. [Calculus playlist: Lesson 36 of 156]

It is sometimes easier to take a double integral (a particular double integral as we'll see) over a region and sometimes easier to take a line integral around the boundary. Green's theorem draws the connection between the two so we can go back and forth. This tutorial proves Green's theorem and then gives a few examples of using it. If you can take line integrals through vector fields, you're ready for Mr. Green.

With traditional integrals, our "path" was straight and linear (most of the time, we traversed the x-axis). Now we can explore taking integrals over any line or curve (called line integrals).

You've done some work with line integral with scalar functions and you know something about parameterizing position-vector valued functions. In that case, welcome! You are now ready to explore a core tool math and physics: the line integral for vector fields. Need to know the work done as a mass is moved through a gravitational field. No sweat with line integrals.

This 17-minute video lesson looks at the iIntuition behind the Mean Value Theorem. [Calculus playlist: Lesson 55 of 156]

Let's jump out of that boring (okay, it wasn't THAT boring) 2-D world into the exciting 3-D world that we all live and breath in. Instead of functions of x that can be visualized as lines, we can have functions of x and y that can be visualized as surfaces. But does the idea of a derivative still make sense? Of course it does! As long as you specify what direction you're going in. Welcome to the world of partial derivatives!

This 8-minute video lecture demonstrates how to use a position vector valued function to describe a curve or path. [Calculus playlist: Lesson 133 of 156]

In this tutorial, we will learn to approximate differentiable functions with polynomials. Beyond just being super cool, this can be useful for approximating functions so that they are easier to calculate, differentiate or integrate. So whether you will have to write simulations or become a bond trader (bond traders use polynomial approximation to estimate changes in bond prices given interest rate changes and vice versa), this tutorial could be fun. If that isn't motivation enough, we also come up with one of the most epic and powerful conclusions in all of mathematics in this tutorial: Euler's identity.

This 8-minute video lesson presents an intuition (but not a proof) of the Squeeze Theorem. [Calculus playlist: Lesson 7 of 156]

You can parameterize a line with a position vector valued function and understand what a differential means in that context already. This tutorial will take things further by parametrizing surfaces (2 parameters baby!) and have us thinking about partial differentials.

You know what Stokes' theorem is and how to apply it, but are craving for some real proof that it is true. Well, you've found the right tutorial!

Finding line integrals to be a bit boring? Well, this tutorial will add new dimension to your life by explore what surface integrals are and how we can calculate them.

This video talka about what is easily one of the most fundamental and profound concepts in statistics and maybe in all of mathematics. And that's the central limit theorem.

This lesson reviews how to change an improper fraction to a mixed number.