Unrestricted Use
CC BY
A graphic for student reference.
- Subject:
- Geometry
- Material Type:
- Student Guide
- Author:
- Cynthia Mantel
- Date Added:
- 06/26/2021
Updating search results...
685 Results
Conditional Remix & Share Permitted
CC BY-NC-SA
This site teaches Geometry to 8th graders through a series of 2398 questions and interactive activities aligned to 19 Common Core mathematics skills.
- Subject:
- Geometry
- Mathematics
- Material Type:
- Activity/Lab
- Interactive
- Provider:
- Khan Academy
- Provider Set:
- Khan Academy
- Date Added:
- 01/09/2015
Conditional Remix & Share Permitted
CC BY-NC-SA
In this module, students learn about translations, reflections, and rotations in the plane and, more importantly, how to use them to precisely define the concept of congruence. Throughout Topic A, on the definitions and properties of the basic rigid motions, students verify experimentally their basic properties and, when feasible, deepen their understanding of these properties using reasoning. All the lessons of Topic B demonstrate to students the ability to sequence various combinations of rigid motions while maintaining the basic properties of individual rigid motions. Students learn that congruence is just a sequence of basic rigid motions in Topic C, and Topic D begins the learning of Pythagorean Theorem.
Find the rest of the EngageNY Mathematics resources at https://archive.org/details/engageny-mathematics.
- Subject:
- Geometry
- Mathematics
- Material Type:
- Module
- Provider:
- New York State Education Department
- Provider Set:
- EngageNY
- Date Added:
- 09/21/2013
Conditional Remix & Share Permitted
CC BY-NC-SA
In Module 3, students learn about dilation and similarity and apply that knowledge to a proof of the Pythagorean Theorem based on the Angle-Angle criterion for similar triangles. The module begins with the definition of dilation, properties of dilations, and compositions of dilations. One overarching goal of this module is to replace the common idea of same shape, different sizes with a definition of similarity that can be applied to geometric shapes that are not polygons, such as ellipses and circles.
Find the rest of the EngageNY Mathematics resources at https://archive.org/details/engageny-mathematics.
- Subject:
- Geometry
- Mathematics
- Material Type:
- Module
- Provider:
- New York State Education Department
- Provider Set:
- EngageNY
- Date Added:
- 10/17/2013
Conditional Remix & Share Permitted
CC BY-NC-SA
In the first topic of this 15 day module, students learn the concept of a function and why functions are necessary for describing geometric concepts and occurrences in everyday life. Once a formal definition of a function is provided, students then consider functions of discrete and continuous rates and understand the difference between the two. Students apply their knowledge of linear equations and their graphs from Module 4 to graphs of linear functions. Students inspect the rate of change of linear functions and conclude that the rate of change is the slope of the graph of a line. They learn to interpret the equation y=mx+b as defining a linear function whose graph is a line. Students compare linear functions and their graphs and gain experience with non-linear functions as well. In the second and final topic of this module, students extend what they learned in Grade 7 about how to solve real-world and mathematical problems related to volume from simple solids to include problems that require the formulas for cones, cylinders, and spheres.
Find the rest of the EngageNY Mathematics resources at https://archive.org/details/engageny-mathematics.
- Subject:
- Geometry
- Mathematics
- Material Type:
- Module
- Provider:
- New York State Education Department
- Provider Set:
- EngageNY
- Date Added:
- 01/06/2014
Conditional Remix & Share Permitted
CC BY-NC-SA
Module 7 begins with work related to the Pythagorean Theorem and right triangles. Before the lessons of this module are presented to students, it is important that the lessons in Modules 2 and 3 related to the Pythagorean Theorem are taught (M2: Lessons 15 and 16, M3: Lessons 13 and 14). In Modules 2 and 3, students used the Pythagorean Theorem to determine the unknown length of a right triangle. In cases where the side length was an integer, students computed the length. When the side length was not an integer, students left the answer in the form of x2=c, where c was not a perfect square number. Those solutions are revisited and are the motivation for learning about square roots and irrational numbers in general.
Find the rest of the EngageNY Mathematics resources at https://archive.org/details/engageny-mathematics.
- Subject:
- Geometry
- Mathematics
- Material Type:
- Module
- Provider:
- New York State Education Department
- Provider Set:
- EngageNY
- Date Added:
- 02/02/2014
Conditional Remix & Share Permitted
CC BY-NC-SA
Module 2 explores two-dimensional and three-dimensional shapes. Students learn about flat and solid shapes independently as well as how they are related to each other and to shapes in their environment. Students begin to use position words when referring to and moving shapes. Students learn to use their words to distinguish between examples and non-examples of flat and solid shapes.
Find the rest of the EngageNY Mathematics resources at https://archive.org/details/engageny-mathematics.
- Subject:
- Geometry
- Mathematics
- Material Type:
- Module
- Provider:
- New York State Education Department
- Provider Set:
- EngageNY
- Date Added:
- 07/05/2013
Conditional Remix & Share Permitted
CC BY-NC-SA
Kindergarten comes to a close with another opportunity for students to explore geometry in Module 6. Throughout the year, students have built an intuitive understanding of two- and three-dimensional figures by examining exemplars, variants, and non-examples. They have used geometry as a context for exploring numerals as well as comparing attributes and quantities. To wrap up the year, students further develop their spatial reasoning skills and begin laying the groundwork for an understanding of area through composition of geometric figures.
Find the rest of the EngageNY Mathematics resources at https://archive.org/details/engageny-mathematics.
- Subject:
- Geometry
- Mathematics
- Material Type:
- Module
- Provider:
- New York State Education Department
- Provider Set:
- EngageNY
- Date Added:
- 11/28/2013
Read the Fine Print
Educational Use
Students are introduced to graphing on the coordinate plane, in the first quadrant, using (x, y) coordinates.
- Subject:
- Geometry
- Mathematics
- Material Type:
- Lesson Plan
- Provider:
- PBS LearningMedia
- Provider Set:
- PBS Learning Media Common Core Collection
- Author:
- U.S. Department of Education
- WNET
- Date Added:
- 07/23/2008
Read the Fine Print
A web page and interactive applet illustrating the properties of a hexagon (6 sided polygon). The applet shows a hexagon where the user can drag any vertex to reshape it. User can see that the interior and exterior angles are constant in a regular hexagon, but vary in an irregular version. Controls allow the display or hiding of the diagonals, and triangles within the hexagon. The web page lists the properties of a hexagon including interior angles, exterior angles, sum of exterior angles, area, number of diagonals and number of internal triangles. Links to pages with generalized properties of all polygons. Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.
- Subject:
- Geometry
- Mathematics
- Material Type:
- Reading
- Simulation
- Provider:
- Math Open Reference
- Author:
- John Page
- Date Added:
- 02/16/2011
Unrestricted Use
CC BY
The goal of this task is to use geometry study the structure of beehives. Beehives have a tremendous simplicity as they are constructed entirely of small, equally sized walls. In order to as useful as possible for the hive, the goal should be to create the largest possible volume using the least amount of materials. In other words, the ratio of the volume of each cell to its surface area needs to be maximized. This then reduces to maximizing the ratio of the surface area of the cell shape to its perimeter.
- Subject:
- Geometry
- Mathematics
- Material Type:
- Activity/Lab
- Provider:
- Illustrative Mathematics
- Provider Set:
- Illustrative Mathematics
- Author:
- Illustrative Mathematics
- Date Added:
- 01/21/2013
Unrestricted Use
Public Domain
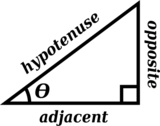
This is a lesson familiarizing students with right triangle trigonometry with applied problem solving.
- Subject:
- Geometry
- Language Education (ESL)
- Material Type:
- Lesson
- Lesson Plan
- Author:
- Ann DeChenne
- Oregon Open Learning
- Date Added:
- 06/16/2022
Read the Fine Print
Educational Use
Students see that geometric shapes can be found in all sorts of structures as they explore the history of the Roman Empire with a focus on how engineers 2000 years ago laid the groundwork for many structures seen today. Through a short online video, brief lecture material and their own online research directed by worksheet questions, students discover how the Romans invented a structure known today as the Roman arch that enabled them to build architecture never before seen by humankind, including the amazing aqueducts. Students calculate the slope and its total drop and angle over its entire distance for an example aqueduct. Completing this lesson prepares students for the associated activity in which teams build and test model aqueducts that meet specific constraints. This lesson serves as an introduction to many other geometry—and engineering-related lessons—including statics and trusses, scale modeling, and trigonometry.
- Subject:
- Geometry
- Mathematics
- Material Type:
- Lesson
- Provider:
- TeachEngineering
- Author:
- Lauchlin Blue
- Malinda Zarske
- Nathan Coyle
- Date Added:
- 02/07/2017
Conditional Remix & Share Permitted
CC BY-NC-SA
This resource was created by Sara Pittack, in collaboration with Lynn Bowder, as part of ESU2's Mastering the Arts project. This project is a four year initiative focused on integrating arts into the core curriculum through teacher education and experiential learning.
- Subject:
- Geometry
- Performing Arts
- Material Type:
- Lesson Plan
- Author:
- Arts ESU2
- Date Added:
- 02/24/2022
Read the Fine Print
An interactive applet and associated web page that show the definition of a horizontal line in coordinate geometry. The applet has two points that the user can drag which define a line. The line flagged when it is horizontal (slope=0) and the equation of the line is shown. The grid, details and coordinates can be turned on and off. The applet can be printed exactly as it appears on the screen to make handouts. The web page has a discussion on how to test for horizontal, the line equation and has links to other pages relating to coordinate geometry. Applet can be enlarged to full screen size for use with a classroom projector. This resource is a component of the Math Open Reference Interactive Geometry textbook project at http://www.mathopenref.com.
- Subject:
- Geometry
- Mathematics
- Material Type:
- Reading
- Simulation
- Provider:
- Math Open Reference
- Author:
- John Page
- Date Added:
- 02/16/2011
Unrestricted Use
CC BY
The purpose of this task is for students to apply the concepts of mass, volume, and density in a real-world context. There are several ways one might approach the problem, e.g., by estimating the volume of a person and dividing by the volume of a cell.
- Subject:
- Geometry
- Mathematics
- Material Type:
- Activity/Lab
- Provider:
- Illustrative Mathematics
- Provider Set:
- Illustrative Mathematics
- Author:
- Illustrative Mathematics
- Date Added:
- 11/13/2012
Unrestricted Use
CC BY
This is a mathematical modeling task aimed at making a reasonable estimate for something which is too large to count accurately, the number of leaves on a tree.
- Subject:
- Geometry
- Mathematics
- Material Type:
- Activity/Lab
- Provider:
- Illustrative Mathematics
- Provider Set:
- Illustrative Mathematics
- Author:
- Illustrative Mathematics
- Date Added:
- 01/20/2013
Unrestricted Use
CC BY
In this problem, the variables a,b,c, and d are introduced to represent important quantities for this esimate: students should all understand where the formula in the solution for the number of leaves comes from. Estimating the values of these variables is much trickier and the teacher should expect and allow a wide range of variation here.
- Subject:
- Geometry
- Mathematics
- Material Type:
- Activity/Lab
- Provider:
- Illustrative Mathematics
- Provider Set:
- Illustrative Mathematics
- Author:
- Illustrative Mathematics
- Date Added:
- 01/20/2013
Unrestricted Use
CC BY
As written, this problem gives students all of the information they need to estimate the thickness of a soda can.
- Subject:
- Geometry
- Mathematics
- Material Type:
- Activity/Lab
- Provider:
- Illustrative Mathematics
- Provider Set:
- Illustrative Mathematics
- Author:
- Illustrative Mathematics
- Date Added:
- 01/04/2013
Unrestricted Use
CC BY
his is a version of ''How thick is a soda can I'' which allows students to work independently and think about how they can determine how thick a soda can is. The teacher should explain clearly that the goal of this task is to come up with an ''indirect'' means of assessing how thick the can is, that is directly measuring its thickness is not allowed.
- Subject:
- Geometry
- Mathematics
- Material Type:
- Activity/Lab
- Provider:
- Illustrative Mathematics
- Provider Set:
- Illustrative Mathematics
- Author:
- Illustrative Mathematics
- Date Added:
- 03/04/2013