This is a SoftChalk that helps my students review the Male Reproduction System.

This activity has students taking the Myers-Briggs personality test.  Once they have taken the personality test they will create a poster highlighting their strengths and weaknesses.  They will also post to a discussion forum with a reflection on their results.

MarketSim helps students understand the functioning of markets by having them become consumers and producers in a simulated economy. There are two versions, both implemented over the internet. Jeremy's market is a consumer barter market. Adam's market introduces firms and money. MarketSim received funding from the National Science Foundation. The simulation is most appropriate for economics principles courses. The principle developers are Tod S. Porter and Kriss Schueller at Youngstown State University.

Fractions and Decimals

Type of Unit: Concept

Prior Knowledge

Students should be able to:

Multiply and divide whole numbers and decimals.
Multiply a fraction by a whole number.
Multiply a fraction by another fraction.
Write fractions in equivalent forms, including converting between improper fractions and mixed numbers.
Understand the meaning and structure of decimal numbers.

Lesson Flow

This unit extends students’ learning from Grade 5 about operations with fractions and decimals.

The first lesson informally introduces the idea of dividing a fraction by a fraction. Students are challenged to figure out how many times a 14-cup measuring cup must be filled to measure the ingredients in a recipe. Students use a variety of methods, including adding 14 repeatedly until the sum is the desired amount, and drawing a model. In Lesson 2, students focus on dividing a fraction by a whole number. They make a model of the fraction—an area model, bar model, number line, or some other model—and then divide the model into whole numbers of groups. Students also work without a model by looking at the inverse relationship between division and multiplication. Students explore methods for dividing a whole number by a fraction in Lesson 3, for dividing a fraction by a unit fraction in Lesson 4, and for dividing a fraction by another fraction in Lesson 6. Students examine several methods and models for solving such problems, and use models to solve similar problems.

Students apply their learning to real-world contexts in Lesson 6 as they solve word problems that require dividing and multiplying mixed numbers. Lesson 7 is a Gallery lesson in which students choose from a number of problems that reinforce their learning from the previous lessons.

Students review the standard long-division algorithm for dividing whole numbers in Lesson 8. They discuss the different ways that an answer to a whole number division problem can be expressed (as a whole number plus a remainder, as a mixed number, or as a decimal). Students then solve a series of real-world problems that require the same whole number division operation, but have different answers because of how the remainder is interpreted.

Students focus on decimal operations in Lessons 9 and 10. In Lesson 9, they review addition, subtraction, multiplication, and division with decimals. They solve decimal problems using mental math, and then work on a card sort activity in which they must match problems with diagram and solution cards. In Lesson 10, students review the algorithms for the four basic decimal operations, and use estimation or other methods to place the decimal points in products and quotients. They solve multistep word problems involving decimal operations.

In Lesson 11, students explore whether multiplication always results in a greater number and whether division always results in a smaller number. They work on a Self Check problem in which they apply what they have learned to a real-world problem. Students consolidate their learning in Lesson 12 by critiquing and improving their work on the Self Check problem from the previous lesson. The unit ends with a second set of Gallery problems that students complete over two lessons.

Students explore methods of dividing a fraction by a unit fraction.Key ConceptsIn this lesson and in Lesson 5, students explore dividing a fraction by a fraction.In this lesson, we focus on the case in which the divisor is a unit fraction. Understanding this case makes it easier to see why we can divide by a fraction by multiplying by its reciprocal. For example, finding 34÷15 means finding the number of fifths in 34. In this lesson, students will see that this is 34 × 5.Students learn and apply several methods for dividing a fraction by a unit fraction, such as 23÷14.Model 23. Change the model and the fractions in the problem to twelfths: 812÷312. Then find the number of groups of 3 twelfths in 8 twelfths. This is the same as finding 8 ÷ 3.Reason that since there are 4 fourths in 1, there must be 23 × 4 fourths in 23. This is the same as using the multiplicative inverse.Rewrite both fractions so they have a common denominator: 23÷14=812÷312. The answer is the quotient of the numerators. This is the numerical analog to modeling.Goals and Learning ObjectivesUse models and other methods to divide fractions by unit fractions

Students use estimation or other methods to place the decimal points in products and quotients. They review the algorithms for the four basic decimal operations and solve multistep word problems involving decimal operations.Key ConceptsThe algorithms for whole-number operations can be extended to decimal operations. Students learned the algorithms for decimal operations in Grade 5. By the end of Grade 6, they should be fluent with these operations.For decimal addition and subtraction, once the decimal points of the addends are aligned (which aligns like place values), the algorithms are the same as for whole numbers. The decimal point in the sum or difference goes directly below the decimal point in the numbers that were added or subtracted.For decimal multiplication and division, one method is to ignore the decimal points and apply the whole-number algorithms. Then use estimation or some other method to place the decimal point in the answer.Goals and Learning ObjectivesReview and practice the algorithms for all four decimal operations.Solve real-world problems involving decimal operations.

Four full-year digital course, built from the ground up and fully-aligned to the Common Core State Standards, for 7th grade Mathematics. Created using research-based approaches to teaching and learning, the Open Access Common Core Course for Mathematics is designed with student-centered learning in mind, including activities for students to develop valuable 21st century skills and academic mindset.

Zooming In On Figures

Unit Overview

Type of Unit: Concept; Project

Length of Unit: 18 days and 5 days for project

Prior Knowledge

Students should be able to:

Find the area of triangles and special quadrilaterals.
Use nets composed of triangles and rectangles in order to find the surface area of solids.
Find the volume of right rectangular prisms.
Solve proportions.

Lesson Flow

After an initial exploratory lesson that gets students thinking in general about geometry and its application in real-world contexts, the unit is divided into two concept development sections: the first focuses on two-dimensional (2-D) figures and measures, and the second looks at three-dimensional (3-D) figures and measures.
The first set of conceptual lessons looks at 2-D figures and area and length calculations. Students explore finding the area of polygons by deconstructing them into known figures. This exploration will lead to looking at regular polygons and deriving a general formula. The general formula for polygons leads to the formula for the area of a circle. Students will also investigate the ratio of circumference to diameter ( pi ). All of this will be applied toward looking at scale and the way that length and area are affected. All the lessons noted above will feature examples of real-world contexts.
The second set of conceptual development lessons focuses on 3-D figures and surface area and volume calculations. Students will revisit nets to arrive at a general formula for finding the surface area of any right prism. Students will extend their knowledge of area of polygons to surface area calculations as well as a general formula for the volume of any right prism. Students will explore the 3-D surface that results from a plane slicing through a rectangular prism or pyramid. Students will also explore 3-D figures composed of cubes, finding the surface area and volume by looking at 3-D views.
The unit ends with a unit examination and project presentations.

Students will extend their knowledge of volume to find the volume of right prisms, seeing that the volume is the area of the base multiplied by the height.Key ConceptsVolume is measured in cubic units. The area of the base of a prism indicates how many cubic units are in the first unit “layer” of the prism. Multiplying by height gives the number of layers, and therefore the volume.GoalsFind the volume of right prisms.SWD: Some students with disabilities may have difficulty connecting newly introduced information with previously learned concepts. Consider ways to help students with disabilities to make connections between what they have learned in previous lessons about volume and right prisms and finding the volume of right prisms.Consider the prerequisite skills for this lesson. Students with disabilities may need direct instruction and guided practice with the skills, measurement, and concepts needed for this lesson.Students should understand these domain-specific terms:volumeright (domain-specific)prismcubicIt may be helpful to preteach these terms to students with disabilities.ELL: As new vocabulary is introduced, be sure to repeat it several times and allow students to repeat after you as needed. Write the new words as they are introduced, and allow enough time for ELLs to check their dictionaries or briefly consult with another student who shares the same primary language if they wish.

Mathematically Productive Instructional Routines (MPIR) are short (10ish minutes), daily exercises aimed at building number sense. These six different MPIR are part of the Mathematically Productive Instructional Routines collection from the Washington Office of Public Instruction and the Washington Association of Educational Service Districts.

The Mathematics Assessment Project is part of the Math Design Collaborative initiated by the Bill & Melinda Gates Foundation. The project set out to design and develop well-engineered tools for formative and summative assessment that expose students’ mathematical knowledge and reasoning, helping teachers guide them towards improvement and monitor progress. The tools are relevant to any curriculum that seeks to deepen students' understanding of mathematical concepts and develop their ability to apply that knowledge to non-routine problems.

Learn about position, velocity, and acceleration in the "Arena of Pain". Use the green arrow to move the ball. Add more walls to the arena to make the game more difficult. Try to make a goal as fast as you can.

This lesson will be a fun way for students to be create and use the collected data to find the measures of central tendency.

This activity is an introduction to meiosis which allows students to understand the basics of meiosis before being given a formal lesson.

The Year is 3016.
Mars has been terraformed and can now sustain human life. You are part of a group of colonizers looking to make a new life for yourselves on the red planet as well as find and utilize resources.

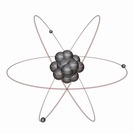
In this lesson, students will learn about the history behind the atomic model and learn how to draw a Bohr model.  To draw the models, cards are provided with examples for students to draw.  Students can use the PhET Simulation:  Build an Atom to check their answers.

The purpose of this assignment is to help you think about what it would’ve been like to have experienced the Mormon Migration. The people who participated in this historic event left many things behind, including their homes, families, jobs, etc.

Students will use the 3-2-1 strategy to analyze "The Most Dangerous Game" by Richard Connell.

This lesson was created by Renste Moeller as part of the Nebraska ESUCC Special Project Digital Age Skills.

After reading “The Most Dangerous Game” students will comb through the text to pull out the best examples of imagery from the story. They will work together in groups of three to collect five examples (per person) of imagery. Students must be able to see each other’s examples, so they don’t repeat them, but also help each other identify which imagery is being documented.